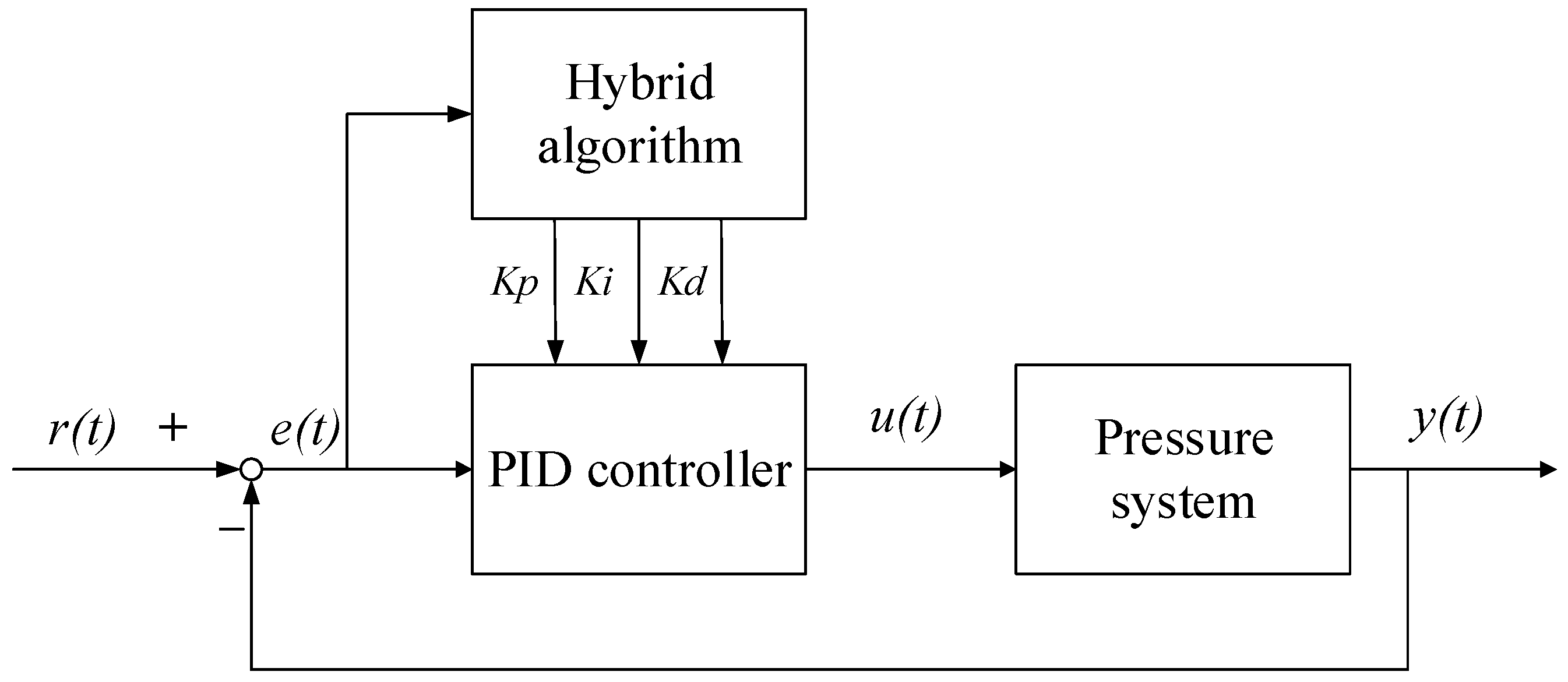
Pid Auto Tuning Procedure

10.01.2021 admin

Pid Auto Tuning Procedure 3,8/5 444 reviews

Pid Auto Tuning Procedure Tool
Auto Tuning.ro
Auto Tuning Video

The Ziegler–Nichols tuning method is a heuristic method of tuning a PID controller. It was developed by John G. Ziegler and Nathaniel B. Nichols. It is performed by setting the I (integral) and D (derivative) gains to zero. The 'P' (proportional) gain, ${displaystyle K_{p}}$ is then increased (from zero) until it reaches the ultimate gain ${displaystyle K_{u}}$ , which is the largest gain at which the output of the control loop has stable and consistent oscillations; higher gains than the ultimate gain ${displaystyle K_{u}}$ have diverging oscillation. ${displaystyle K_{u}}$ and the oscillation period ${displaystyle T_{u}}$ are then used to set the P, I, and D gains depending on the type of controller used and behaviour desired:

Essentially, the PID controller “learns” how the process responds to a disturbance or change in set point, and calculates appropriate PID settings. In the case of a temperature controller like OMEGA’s Platinum series, when “Auto Tune” is selected the controller activates an output. Mar 22, 2016 Centroid CNC control DC Servo Motor PID Tuning Procedure. This video takes you thru the step by step process and finer details or tuning a DC Servo Motor with a Centroid CNC control using CNC11.

Pid Auto Tuning Procedure Tool

Ziegler–Nichols method^[1]
Control Type	${displaystyle K_{p}}$	${displaystyle T_{i}}$	${displaystyle T_{d}}$	${displaystyle K_{i}}$	${displaystyle K_{d}}$
P	${displaystyle 0.5K_{u}}$	–	–	–	–
PI	${displaystyle 0.45K_{u}}$	${displaystyle T_{u}/1.2}$	–	${displaystyle 0.54K_{u}/T_{u}}$	–
PD	${displaystyle 0.8K_{u}}$	–	${displaystyle T_{u}/8}$	–	${displaystyle K_{u}T_{u}/10}$
classic PID^[2]	${displaystyle 0.6K_{u}}$	${displaystyle T_{u}/2}$	${displaystyle T_{u}/8}$	${displaystyle 1.2K_{u}/T_{u}}$	${displaystyle 3K_{u}T_{u}/40}$
Pessen Integral Rule^[2]	${displaystyle 7K_{u}/10}$	${displaystyle 2T_{u}/5}$	${displaystyle 3T_{u}/20}$	${displaystyle 1.75K_{u}/T_{u}}$	${displaystyle 21K_{u}T_{u}/200}$
some overshoot^[2]	${displaystyle K_{u}/3}$	${displaystyle T_{u}/2}$	${displaystyle T_{u}/3}$	${displaystyle 0.666K_{u}/T_{u}}$	${displaystyle K_{u}T_{u}/9}$
no overshoot^[2]	${displaystyle K_{u}/5}$	${displaystyle T_{u}/2}$	${displaystyle T_{u}/3}$	${displaystyle (2/5)K_{u}/T_{u}}$	${displaystyle K_{u}T_{u}/15}$

The ultimate gain ${displaystyle (K_{u})}$ is defined as 1/M, where M = the amplitude ratio, ${displaystyle K_{i}=K_{p}/T_{i}}$ and ${displaystyle K_{d}=K_{p}T_{d}}$ .

These 3 parameters are used to establish the correction ${displaystyle u(t)}$ from the error ${displaystyle e(t)}$ via the equation:

{displaystyle u(t)=K_{p}left(e(t)+{frac {1}{T_{i}}}int _{0}^{t}e(tau ),dtau +T_{d}{frac {de(t)}{dt}}right)}

which has the following transfer function relationship between error and controller output:

{displaystyle u(s)=K_{p}left(1+{frac {1}{T_{i}s}}+T_{d}sright)e(s)=K_{p}left({frac {T_{d}T_{i}s^{2}+T_{i}s+1}{T_{i}s}}right)e(s)}

Evaluation[edit]

The Ziegler–Nichols tuning (represented by the 'Classic PID' equations in the table above) creates a 'quarter wave decay'. This is an acceptable result for some purposes, but not optimal for all applications.

This tuning rule is meant to give PID loops best disturbance rejection.^[2]

It yields an aggressive gain and overshoot^[2] – some applications wish to instead minimize or eliminate overshoot, and for these this method is inappropriate. In this case, the equations from the row labelled 'no overshoot' can be used to compute appropriate controller gains.

References[edit]

^Ziegler, J.G & Nichols, N. B. (1942). 'Optimum settings for automatic controllers'(PDF). Transactions of the ASME. 64: 759–768.Cite journal requires journal= (help)
^ ^a^b^c^d^e^fZiegler–Nichols Tuning Rules for PID, Microstar Laboratories

Bequette, B. Wayne. Process Control: Modeling, Design, and Simulation. Prentice Hall PTR, 2010. [1]
Co, Tomas; Michigan Technological University (February 13, 2004). 'Ziegler–Nichols Closed Loop Tuning'. Retrieved 2007-06-24.

External links[edit]

Auto Tuning.ro

Auto Tuning Video

Retrieved from 'https://en.wikipedia.org/w/index.php?title=Ziegler–Nichols_method&oldid=949638647'

4reeaus41n.netlify.app